We wrapped up the first part of this series focusing on how a neural network connects and interacts with each of its respective layers. To take a step back though, let’s recap and talk about the big picture: how a neural network is relevant to machine learning and what it ultimately accomplishes. We talked about how machine learning is basically a program that continuously trains itself on data to produce more accurate outputs based on its intended purpose. In the example of the puzzle we gave in part 1, the expectation would be that by the time the program has run a 1000 times it should be able to identify each piece accurately and quickly. This is done by leveraging the neural network inside the program to make accurate decisions on which piece is which. To get to those accurate decisions though, we have to train our program. This is done by adjusting the weights and biases associated with the neurons from layer to layer, which brings us to the topic of part 2.
Before we dive into what weights and biases are and how they impact the overall neural network, let’s talk about the composition of a layer and its respective neurons. This is critical to understanding the subject of weights and biases. A layer is composed of neurons intended to identify one specific feature of our program. The information about the feature a layer is looking for will be used to inform other layers looking for their own specific features. As the information of features by each layer is aggregated in sum, the program produces an answer aligned closest to what it has gathered from all layers. In the case of the puzzle there will be a layer looking for flat sides, there will be a layer looking for if a piece has a single tab, two tabs, no tabs, red, blue, yellow, and so on to determine what each piece of the puzzle is.
Where the neurons of a layer come into play, is a layer will have multiple neurons within a single layer. Each neuron receives the same input information, however, they are all analyzing the information differently,while still working together, to come up with the most accurate answer for the intended feature that layer is looking for. If we go back to the puzzle example and use the layer looking for flat sides, some of the neurons will specifically look for flat sides and say “yup, we got a flat side over here”. At the same time, neurons within that same layer may be looking for tabs or rounded sides and say “hey, we don’t have any tabs or rounded sides”. Taking the information gathered by the neurons, the layer has learned that there is a flat side, and there are no rounded sides, which means it can confidently assert that the layer has successfully identified a flat side. This layer will then pass that information along to the next layer. We use weights and biases to continuously fine tune our program by telling the program when it’s right or wrong. Think of weights and biases similar to knobs that are constantly being tweaked to produce a more accurate over time.
When we say weights and biases, this refers to the importance we put on the connection between layers of our neural network and what we tell our neurons inside the layers based on what we design the program to accomplish. The weights piece focuses on the connections we have between layers. Without going too much into the math, we can think of the weight we apply to a connection between two layers as us telling the program hot or cold. If hot is represented by the number 1 and cold is the number 0, the hotter we make a connection the more we influence the program to look for a specific element. In the instance of first trying to identify a corner piece we would put more weight on a successfully identified flat side. So we’re essentially saying if a layer identifies a flat side, we will put more emphasis on the communication to the next layer noting a flat side has been identified. We’re going to skip over the details, but if you are interested in learning more about the actual math on how this works, the sigmoid function is how weights are applied on a log curve. The resources I linked in the first part all cover this in detail, plus more.
If you recall from part one, we compared layers to filters in a neural network. A layer will have multiple neurons that essentially act as a number holder for an evaluation technique that is used to assess each neuron against all the other neurons in the layer. It will provide relevant information to the other layers using some advanced math (sigmoid function, plus more). We’ll talk about how this is used later on. Now, let’s go back to our puzzle example. If the goal of our program is to solve a puzzle and we want the program to start looking for corner puzzle pieces, we would put an emphasis on having connections that have flat sides. To apply this logic we would tell our program at the first layer if you see something that looks like a flat side, it may be a corner piece and to pass that info along to the next layer. We do this by putting more weight on the connections that look for flat sides.
You may think, “Well why don’t we make it yes or no if it has a flat side and pass it along?” Well, that’s an option if we were only looking for corner pieces but in this case there will be other pieces of the puzzle that we’ll need to identify such as a middle piece with no flat sides. This is accounted for by organizing our neurons to communicate based on how we assign our layers to look for things. Take a look at the graphics below. In the first graphic we have that first layer that has received a corner piece. The first layer is looking for flat sides and we’ve put weight on flat sides to basically tell this layer, hey we have some flat sides, pass this info along to the next layer which fires the highlighted neurons in red. In the second graphic, we pass in a middle piece with no flat sides. This gets passed along to the next layer firing different neurons in blue. Go back to what we explained at the beginning of the post. Same layer is looking at the same inputs, however each neuron is analyzing that information differently. The blue neurons are looking for non-flat sides. Red neurons are looking for flat sides and since we care more about flat sides, we put a higher weight on this connection to inform the next layer that we have identified a flat portion of a puzzle piece and this is now more likely to be a corner piece.
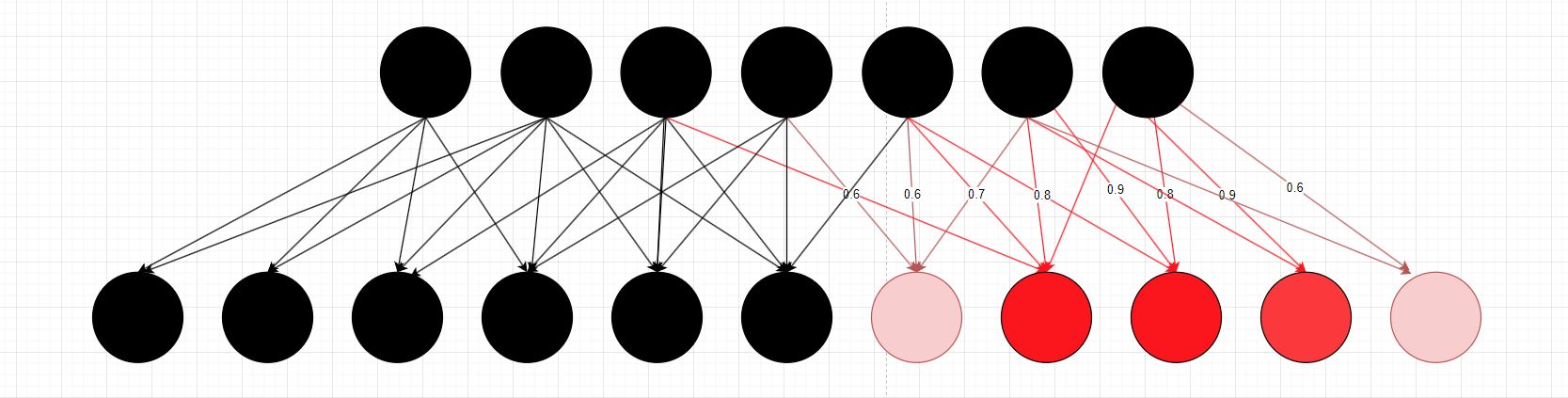 Figure (Neurons Firing in Red)
Figure (Neurons Firing in Red)
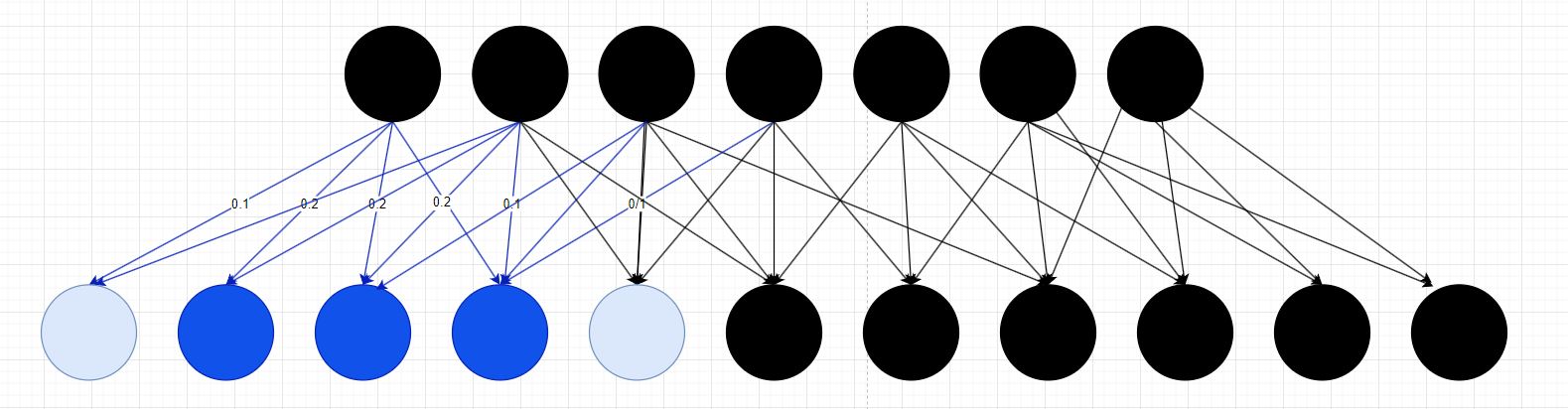 Figure (Neurons Firing in Blue)
Figure (Neurons Firing in Blue)
If it still feels a bit confusing on what a weight is, the other analogy to think of is a two sided balance scale. If you put more weight on one side, the scale will tip that way. If you put more weight on the other side of the scale then vice versa. We apply this logic as a way to help train our program on how it should think.
Ok so we’ve covered weights quite a bit, but Maho, you mentioned something about biases in the beginning and all this weight talk sounds an awful lot like biases. Well you’re sort of right. Weights and biases are similar in that we are essentially telling the program what it should be caring about. So, what is a bias? A bias is how we leverage the neurons in a layer to say what or what not to look for. The bias helps us get closer to that 1 or 0 that tells our layers this is what we should be caring about. From a mathematical perspective it acts sort of like a negative effect.
Weights are the connections between layers that pass along information from layer to layer based on what we want each layer to focus on. Bias is how we fine-tune the neurons in each layer to then pass along the information from layer to layer. If we go back to our puzzle example, we used an example of looking for a corner piece. That first layer is checking to see if the piece has a flat side. Well, how that layer determines if a side is flat is effectively the neurons with appropriate bias at play. We tell the neurons in the layer to have a certain bias using math to look for sides that are flat and should be a piece of the puzzle. Similar to telling weight if it’s hot or cold, bias uses a similar method to check if something aligns to the expected outcome. If the piece had a flat side and was red, there would be numbers assigned to where the piece was flat close to 1, where if there was curvature or nothing at all suggesting not part of the piece it would trend negative closer to 0. Use the below graphic to help visualize this.
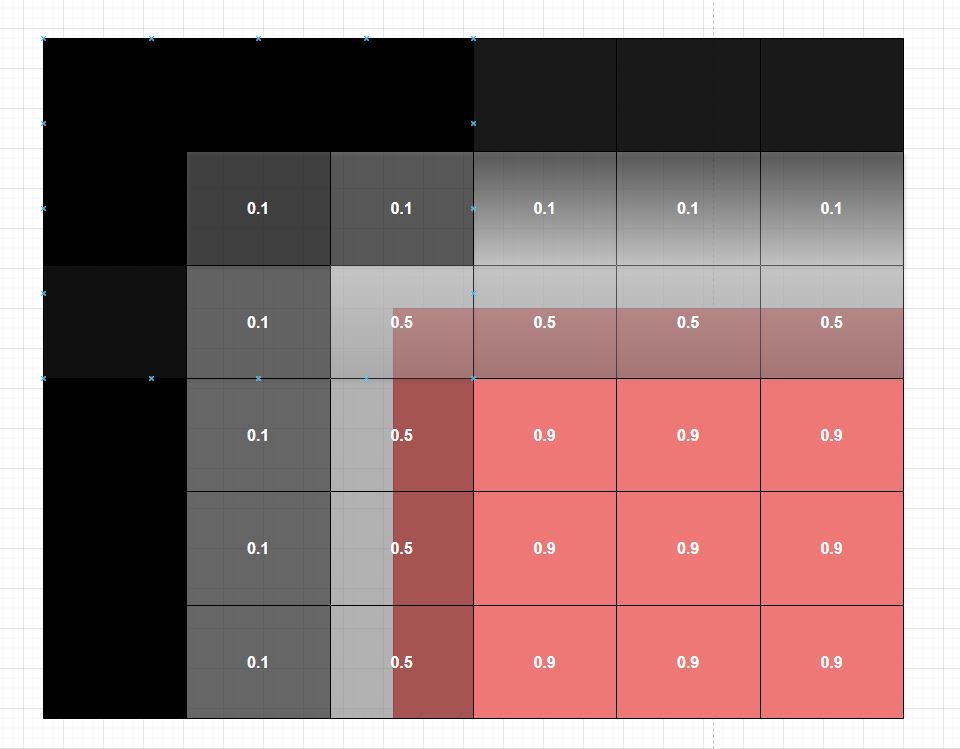 Figure (Bias Visualized with Numbers)
Figure (Bias Visualized with Numbers)
The bias plays a critical part in training our neural network / machine learning program as this is what we can continuously fine-tune to make predictions more accurate. The closer a bias has to 1, the more likely it is that that neuron is identifying the correct thing it has been told to look for. The further away from 1 or you can think of as closer to 0, the program is identifying something that is not what it is supposed to be looking for. In the next part, we’ll cover how to further train and enhance the accuracy of our models. As a sneak peak, just know that it has to do with adjusting biases and weights to tell our program when it is or isn’t correct. Keep in mind that bias and weight all feed into some more advanced math, but the key point is that this is how we train neural networks / machine learning programs over time to further refine accuracy.
So, let’s summarize what we’ve learned up to this point. A neural network is the foundational piece of how machine learning works, which is designed to replicate how neurons in our brain work. The neural network is composed of layers, with a number of neurons in each layer. Each layer is designed to perform a very specific function based on what the neurons in each layer are programmed to look for. Each layer is connected to one another and leverages weights to inform, layer to layer, what the program is looking for. Bias is how we tell our neurons if it is or isn’t looking at the right thing. By leveraging weights and biases, we are able to train our program to be more accurate as it communicates through the layers.
Hopefully you’ve been able to follow along up to this point and if something isn’t making sense, please let me know! Also, feel free to check out the material I linked in the first post as that goes much deeper into specifics and contains a lot of helpful supplementary information. The next post will dive into the meat of how a program continuously trains itself over time to produce more accurate outcomes.
Next up for final article: Machine Learning Part 3!
Previous Article: Machine Learning Part 1!
